| Definition |
Wenn die Summe aller Teiler einer natürlichen Zahl n gleich 2n ist, so spricht man von einer vollkommenen Zahl.
k vollkommene Zahl Û s(k)=2k Û s(k)-k=k
|
| Beispiel 1 |
Die ersten vollkommenen Zahlen sind 6, 28, 496, 8128, 33550336, ...,denn
s(6)=1+2+3+6=12=2*6
s(28)=1+2+4+7+14+28=56=2*28
s(496)=496
s(8128)=8128
|
| Satz 1 |
Alle Vielfachen einer vollkommenen Zahl sind abundante Zahlen.
|
| Beispiel 2 |
6 ist vollkommene Zahl
3*6=18 hat die Teilermenge T={1, 2, 3, 6, 9, 18} und
s(18)=1+2+3+6+9+18=39>2*18=36
|
| Satz 2 |
Keine Primzahl p ist eine vollkommene Zahl, denn s (p)=1+p<2p. Für eine vollkommene Zahl k gilt also s (k)>1+k und somit 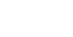 . .
|
| Beispiel 3 |
13 ist Primzahl und s(13)=1+13=14<2*13=26
|
| Satz 3 |
Für eine vollkommene Zahl k gilt s (k)=2k und somit 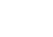 . .
|
| Beispiel 4 |
s(28)=1+2+4+7+14+28=56=2*28
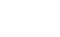
|
| Satz 4 |
Eine ganzzahlige Potenz einer Primzahl k=pa ist keine vollkommene Zahl.
Beweis:
Die Teilermenge T dieser Zahl ist T(pa)={1, p, p2, p3, ..., pa}, also
s (k)-k=s (pa)-pa=1+p+p2+p3+ ...+pa-1=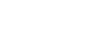 . .
Für p=2 ist der Nenner gleich 1 und sonst größer 1, also ist
|
| Beispiel 5 |
k=113, dann gilt T(113)=T(1331)={1, 11, 121, 1331} und s(1331)=1464¹2662.
|
| Satz 5 |
(Euler) Falls p=2n-1 eine Primzahl ist, so ist  eine vollkommene Zahl. eine vollkommene Zahl.
Beweis:
Per Definition ist q eine vollkommene Zahl, genau dann wenn s (q)=2q=p(p+1). Nun gilt aber  , da , da  nach Satz 2 "Sigmafunktion", denn die erste Zahl ist nur durch 2 teilbar und die zweite Zahl nicht. nach Satz 2 "Sigmafunktion", denn die erste Zahl ist nur durch 2 teilbar und die zweite Zahl nicht.
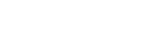 nach Satz 2 "Sigmafunktion". nach Satz 2 "Sigmafunktion".
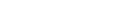 , da p Primzahl und deshalb nur durch p und 1 teilbar ist. , da p Primzahl und deshalb nur durch p und 1 teilbar ist.
Insgesamt folgt also s (q)=2q=p(p+1) und somit ist q vollkommen.
|
| Folgerung |
Falls es unendlich viele Mersenne-Primzahlen gibt, so gibt es auch unendlich viele vollkommene Zahlen.
|
| Satz 6 |
Jede gerade vollkommene Zahl a ist von der Art 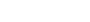 . .
Beweis:
Sei a eine gerade vollkommene Zahl. Wähle a=2n-1u mit u ungerade. Dann gilt:
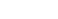 da a vollkommen, also da a vollkommen, also 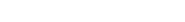 nach Satz 2 "Sigmafunktion", denn 2n und u sind teilerfremd. Nach dem selben Satz gilt dann: nach Satz 2 "Sigmafunktion", denn 2n und u sind teilerfremd. Nach dem selben Satz gilt dann:
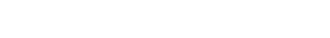
und somit
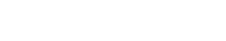 . .
Also sind u und 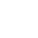 Teiler von u und somit ist Teiler von u und somit ist 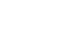 und u eine Primzahl, denn u hat nur diese 2 Teiler. Also muss gelten u=2n-1, was zu beweisen war. und u eine Primzahl, denn u hat nur diese 2 Teiler. Also muss gelten u=2n-1, was zu beweisen war.
|
| Beispiel 6 |
p=22-1=4-1=3 ist eine Primzahl, also ist 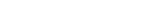 eine vollkommene Zahl. eine vollkommene Zahl.
p=23-1=8-1=7 ist eine Primzahl, also ist 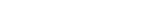 eine vollkommene Zahl. eine vollkommene Zahl.
|
| Satz 7 |
Jede vollkommene Zahl ist die hintereinander folgende Summe von k natürlichen Zahlen beginnend bei 1.
s (k)=2k Þ $ lÎ IN: 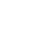
Beweis:
Jede vollkommene Zahl a hat die Gestalt 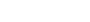 . Nach Satz 1 Sechseckszahlen hat eine Sechseckszahl Hk die Gestalt Hk=k(2k-1). Wenn man k=2n-1 setzt, dann ist 2k=2n und somit ist eine vollkommene Zahl eine Sechseckszahl. Jede Sechseckszahl ist aber die Summe der ersten l natürlichen Zahlen nach Folgerung Sechseckszahlen. . Nach Satz 1 Sechseckszahlen hat eine Sechseckszahl Hk die Gestalt Hk=k(2k-1). Wenn man k=2n-1 setzt, dann ist 2k=2n und somit ist eine vollkommene Zahl eine Sechseckszahl. Jede Sechseckszahl ist aber die Summe der ersten l natürlichen Zahlen nach Folgerung Sechseckszahlen.
|
| Beispiel 7 |
6=1+2+3
28=1+2+3+4+5+6+7
496=1+2+...+31
8128=1+2+...127
|
| Geschichte |
Es ist bis heute nicht bekannt, ob es eine ungerade vollkommene Zahl gibt. Folgende Teilergebnisse sind bisher gezeigt worden:
Euler: Eine ungerade vollkommene Zahl u ist von der Form u=p4a+1q2, wobei p eine ungerade Primzahl ist, die relativ prim zu q ist, also teilerfremd zu q.
1887 nahm Sylvester an und 1925 bewies Gradshtein, dass jede ungerade vollkommene Zahl mindestens 6 unterschiedliche Primfaktoren haben muss.
1987 zeigten Ball und Coxeter, dass jede ungerade vollkommene Zahl mindestens 8 unterschiedliche Primfaktoren haben muss, wenn sie nicht durch 3 teilbar ist.
1888 zeigte Catalan, dass wenn eine ungerade vollkommene Zahl nicht durch 3, 5 oder 7 teilbar ist, dann hat sie mindestens 26 unterschiedliche Primfaktoren.
Brent, Cohen Riele 1991: Eine ungerade vollkommene Zahl ist größer als 10300.
Brandstein 1982: Der größte Primfaktor einer ungeraden vollkommenen Zahl ist größer als 500000.
Sayers 1986: Eine ungerade vollkommenen Zahl hat mindestens 29 Primfaktoren.
Stuyvaert zeigte 1896, dass eine ungerade vollkommene Zahl eine Summe von Quadraten sein muss.
1891 Lucas: Alle geraden vollkommenen Zahlen außer 6 enden mit den Ziffern 16, 28, 36, 56 oder 76.
|
| Satz 8 |
1891 Lucas: Alle vollkommenen Zahlen außer der 6 haben die digitale Wurzel 1.
|
| Beispiel 8 |
33550336 ist eine vollkommene Zahl
3+3+5+5+0+3+3+6=28
2+8=10
1+0=1
33550336 hat die digitale Wurzel 1
|
| Satz 9 |
Für jede vollkommene Zahl v gilt
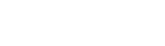
|
| Beispiel 9 |
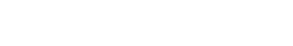
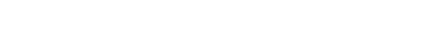
|
| Satz 10 |
Die Summe der Kehrwerte aller Teiler einer vollkommenen Zahl ist 2.
Beweis:
Habe n die Teilermenge T={a1, a2, a3, a4, ... ak-1, ak} mit ak-1=1 und ak=n. Dann gilt
n=a1*a2=a3*a4= ... =ak-1*ak und somit
s(n)=a1+a2+a3+a4+ ... +ak-1+ak=2n, da n vollkommene Zahl
s(n)=a1+a2+a3+a4+ ... +1+n=2n
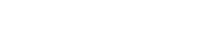
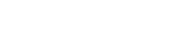
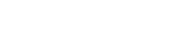 , weil n=a1*a2 und so weiter. , weil n=a1*a2 und so weiter.
|
| Beispiel 10 |
28 hat die Teilermenge T28={1, 2, 4, 7, 14, 28}={2, 14, 4, 7, 28, 1}
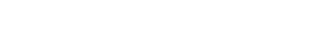
|
| Satz 11 |
(Eaton 1995) Jede gerade vollkommene Zahl v>6 kann durch Dreieckszahlen Tn dargestellt werden nach: v=1+9Tn=T3n+1 wobei n=8j+2
|
| Beispiel 11 |
Tn hat die Werte 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ...
Sei v=28=1+9T2=1+9*3=1+27 und 2=8*0+2
Sei v=496=1+9T10=1+9*55=1+495 und 10=8*1+2
und
Sei v=28=T3n+1=T7 mit n=2
>Sei v=496=T3n+1=T31 mit n=10, denn 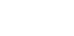 . .
|